Key Takeaways
- Reopening businesses and schools will require reliable testing data.
- Frequent testing is an obvious solution, but costs will be prohibitive and supply may be limited.
- Pooled testing offers a cost-effective and scalable solution, wherein tests are batched to test multiple individuals simultaneously.
- Pooled testing could ramp up the number of tests while lowering testing costs, especially in low-prevalence areas.
- Schools and businesses saddled with testing costs could lower costs by half or even threequarters.
Read the press release about the study here.
Abstract
In the coming weeks and months, decisions about reopening businesses and schools while keeping employees and customers safe will likely fall to business leaders and school administrators. While frequent testing might seem like the natural answer, costs will quickly add up for American businesses and school systems already crippled in the aftermath of a major shutdown. Finding cost-effective ways to test might provide a way out of the shutdown.
“Pooled testing” is a well-established approach to track infectious disease, wherein a lab tests batched samples of several people for the presence of active virus.1 If the test indicates at least one person in that pool is infected, repeat testing of the individuals in the infected pool can reveal the source. In contrast, if the pooled sample comes back negative, it could clear all members of the pool for work, at least until the next testing cycle. While there are inherent challenges in this approach, including choosing appropriate pool sizes and factoring in test-reliability concerns, our estimates suggest that pooled testing could lower testing costs by half or even three-quarters for many schools and businesses. Greater savings are incurred in low-prevalence areas. Employers need to identify COVID-19+ workers and do so at reasonable cost. Pooled testing is an effective tool for doing so.
Introduction
Several states are starting to reopen businesses, starting with small businesses in Georgia.2 But many schools and large businesses remain closed, and the prospects for a return to school in the fall are unclear. Eventually, America will need to get back to business; the question is how.
Some have called for broad-based government testing — perhaps by the military.3 A more likely scenario is that employers will have flexibility in how they protect their customers and workforce. The Occupational Safety and Health Administration, for example, has issued guidance on preparing workplaces, but these are “advisory in nature.”4
Thus, decisions about reopening will likely be left to business leaders and school administrators. The decision process is unclear, but clearly depends on finding ways to identify anyone infected and keep them at home, where they will not spread the disease to other students, employees, or customers. Frequent testing seems like the natural answer. Yet, with current lab fees around $100 per test, repeatedly administering COVID-19 tests to an entire workforce or student body will become prohibitively costly for employers and schools already reeling from major economic dislocation.5 Moreover, the country likely doesn’t possess the capacity to test every worker or student.
The Trump administration recently announced a strategy — in partnership with state and local governments and the private sector — to increase capacity to enable testing of 2 percent of the population.6,7 This is a step in the right direction, but some researchers estimate we need at least 5 million tests per day to begin reopening the economy, and 20 million or more per day to fully remobilize.8 Despite recent advances, testing capacity still lacks sorely behind this demand.
In this working paper, we propose a scientifically feasible method to save money and scarce testing resources. “Pooled testing” is a long-established approach to tracking infectious disease, and has already been run successfully on coronavirus samples at labs in Stanford and Israel.1,9,10 Employers and school systems would do well to explore the results. By pooling, labs should be able to scale up to millions of tests per day using existing sequencing infrastructure, according to researchers at Harvard and MIT — far more than the country has achieved as of this writing.11 The science is not new, so almost any lab can adopt the protocols.
In pooled testing, specimen samples from several people are combined into a single pool. If none of the workers or students within the pool is positive, the pooled sample will come back negative and clear all of them for normal activities. On the other hand, if the test indicates at least one person in that pool is infected, further testing is performed on each individual in that pool. This follow-up step does not require a separate round of specimen collection. Rather, each person’s sample is split into two at the beginning of the process – one is subjected to pooled testing, and the other set aside in case individual follow-up testing is required.
This strategy can be used with polymerase chain reaction (PCR) testing designed to determine whether someone is currently infected.i PCR testing can be used to isolate and quarantine those with active infections. The most efficient initial pool size depends on prevalence, with rarer conditions allowing larger pools.12 Given the current prevalence of COVID19, even 5–10-person pools of employees or students are likely to test negative, obviating the need for administering tests to each person. A recent study suggests that it is feasible to pool samples on this scale without significantly compromising the integrity of the PCR tests.13
A simple example illustrates the logic. Consider an employer with 100 employees in a region of the country believed to suffer from 5 percent prevalence of active COVID-19 infection. This employer splits up its workforce into 20 groups of five workers each. For simplicity, suppose that exactly five workers have the disease, so that the employer is experiencing the same prevalence as its overall region. Under pooled testing, no more than five pools will return positive tests. The employer then tests the employees in the positive pools individually. In this case, no more than 25 individual tests are run, since there are five pools testing positive, each with five workers. Ultimately, the employer has successfully identified all five of its COVID-19+ employees, but it only needed to run 45 tests — 20 initial pooled tests and 25 individual follow-up tests. The employer saved 55 percent of the cost that would have been incurred via individualized testing.ii
Pooled testing works best when the employer or school system chooses pool sizes correctly. For instance, if pools are set too large, every pool might test positive. In this case, the employer gains nothing from that round of pooled tests. This issue is particularly salient in high-prevalence regions, where large pools of employees might routinely turn up at least one positive case.
By contrast, employers in lower-prevalence regions can afford to use larger pools, because even large pools of employees have a good chance of testing negative in these regions. However, even relatively high-risk regions stand to gain from pooled testing. For example, pool sizes of four to seven employees could help the vast majority of employers reap most of the gains from pooled testing, even when they are highly uncertain about the prevalence of the illness in their workforce.
We estimate that pooled testing could reduce testing costs by 80 percent in low-prevalence regions, and still save 50 percent for higher prevalence (5 percent) locations. Indeed, even if prevalence eventually climbs to 10 percent, well above any current estimates, employers can save as much as 40 percent via pooled-testing strategies.
The Economics of Pooled Testing
Employers need to identify all their COVID-19+ workers and do so at minimum cost. We develop a simple model that identifies the optimal pool size to minimize the total cost of testing to the employer. We then quantify the savings to employers from pooled testing under the optimal pool size and under simple rules of thumb for employers that are uncertain about the prevalence of active infections in their workforce.
As with all diagnostics, COVID-19 tests are imperfect. In particular, several recent studies suggest that the sensitivity of PCR tests on samples collected by nasal swab is around 70 percent — meaning that about 3 in 10 infected patients will return a negative test result.14,15 Much of this error is driven by factors related to sample collection (e.g., the patient doesn’t have high enough viral-load levels at the time of collection or the swab didn’t reach the right place) rather than failures of the PCR test itself.16 But the costs of a false negative in this situation can be quite large — if someone believes they are free of disease when actually they are not, they risk spreading the disease to other employees, customers or students — the exact scenario that testing is trying to prevent. Ideally, testing sensitivity will improve with time; in the meantime, employers can combine diagnostic testing with other strategies, such as symptom monitoring and contact tracing. Later, we explore how imperfect test reliability can be managed and mitigated in the context of pooled testing. To start, we consider the simpler case of pooling with a perfect test. This simple, stylized case nonetheless neatly demonstrates the qualitative relationships among pool sizes, costs and infection rates.
We consider an employer with N workers. We confine our attention to a two-stage pooling strategy. In the first stage, the employer splits up its workforce into groups of equal size. In the second stage, the employer runs individual tests on all workers who belonged to groups that test positive. It is relatively easy to adapt and apply this framework to strategies with more than two stages. For example, employers in very low-prevalence regions might choose to run several rounds of pooled testing before taking the costly step of individual testing. For example, an employer might start with pools of 30 workers. Among the pools that test positive, it might then test subsets of 10 workers each to identify the remaining groups that require individualized tests. The conceptual results we derive here are applicable to these multistage strategies: Lower-prevalence regions can afford to test larger pools and can afford to field multiple pooled testing rounds before beginning individualized testing. Moreover, employers can learn over time from the prevalence level revealed in an initial round of testing. If prevalence is higher or lower than expected, pool size can be adjusted in the next round.17
We also assume for simplicity that workers are homogeneous in their risk of testing positive. This is without loss of generality, as the employer could simply stratify its workforce into subgroups by risk, performing the cost-minimization problem below on each of the subgroups individually. For example, it could first split up its workforce into those who have traveled to high-risk areas or encountered infected people, and those who have not. Since the prevalence of the illness is likely higher in the first group than the second, pool sizes ought to be smaller in the first group than the second. The analytic framework below could be separately applied to each group of workers.
Each round of testing costs τC . This could be interpreted literally as a single test, or more generally as a testing protocol. For example, some employers might choose to conduct two consecutive tests on the same worker or group of workers; if at least one of these is positive, the employer might deem that group or worker to be positive. Sequential testing strategies could help mitigate the problem of false negatives, which is especially troublesome in this case. We consider this approach later when we discuss imperfect testing reliability. If a pool of workers tests positive, all workers within that pool then receive an individual round of testing, each of which also costs τC . This may be a conservative assumption, because the round of follow-up testing might be cheaper. Novel sequencing technology holds the promise of using genetic “bar codes” to identify which individual(s) in a pooled sample triggered the positive test. This would eliminate the need to collect a follow-up individual sample.11
We suppose the prevalence of active infection in the workforce is π. In our initial development, we assume the employer knows prevalence with certainty, even though it does not know the identity of the infected workers. In our numerical analyses, we explore the consequences of uncertainty and show that, while uncertainty is costly, employers can still save considerable resources from simple pooled testing strategies even when prevalence is unknown.
We also suppose the pool size is set at P. Therefore, (N/P ) pooled tests are originally run. For instance, an employer with 100 workers choosing a pool size of five will run 20 initial pooled tests. Moreover, the probability that a pool of P workers contains at least one infected member is 1-(1-π)P. Note that (1-π)P is the probability that all workers in the pool test negative.iii The expected number of pools testing positive is given by (1-(1-π)P)(N/P ). All P members of these COVID-19+ pools will be tested individually. Therefore, the expected number of workers receiving follow-up tests will be P *(1-(1-π)P)(N/P ) = (1-(1-π)P)N.
In light of the expressions above, the total cost of the pooled testing approach will be:
T(P;π) = ((NτC)/P ) + (1-(1-π)P(NτC).
Because total costs are proportional to NτC, the pool size minimizing the total cost of testing is the same as the pool size minimizing (T(P;π)/NτC ), namely the number of tests per worker. Employing this logic and dropping constants from the minimization problem yields our objective function, which minimizes the number of tests per worker:
min(N≥P≥1) [(1/P ) -(1-π)P ].
Analytical optimization is challenging because the optimal pool size has to be an integer. Therefore, we solve this problem numerically in the subsequent section. Nonetheless, calculus provides us with some intuition for how pool sizes change. Employing the simplifying assumption of continuous pool sizes, we can show the following:
- Provided we are at an optimal pool size, higher prevalence never results in larger pool sizes.iv Intuitively, when the prevalence is higher, enlarging each pool makes it even more likely that the entire pool will test positive and necessitate a costly round of follow-up testing.
- Higher prevalence reduces the savings generated by a pooled testing approach.v In the case of a perfectly reliable test, when illness prevalence is less than or equal to 30 percent, pools of three or more are helpful.vi
Pool Sizes
We solve numerically for the integer-valued pool sizes that minimize the cost function above, and we study how these optimal pool sizes vary with the active infection rate, π.vii Figure 1 presents the optimal integer-valued pool sizes chosen by an employer who knows the overall COVID-19 infection rate in its workforce. This should be viewed as the theoretical maximum savings that can be generated by pooled testing.
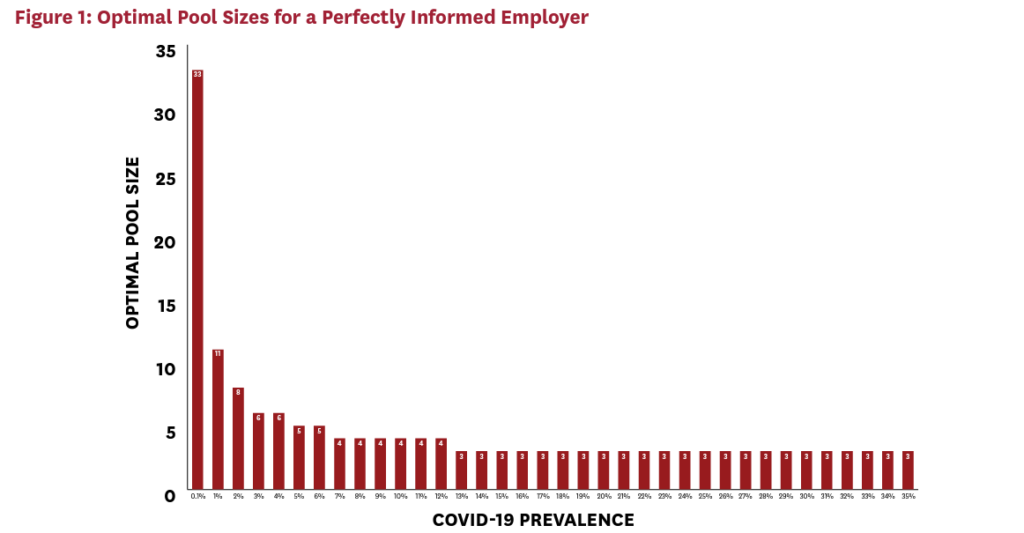
After an initially rapid decline, optimal pool size falls rather slowly with increasing COVID-19 prevalence. This has important implications for employers who face uncertainty about the underlying rate of COVID-19. For example, an employer who predicts an underlying prevalence of 5 percent will achieve nearly optimal outcomes so long as the actual prevalence lies between 3 percent and 30 percent. That is, the employer’s forecast can be wrong by 40 percent or more without major cost consequences.
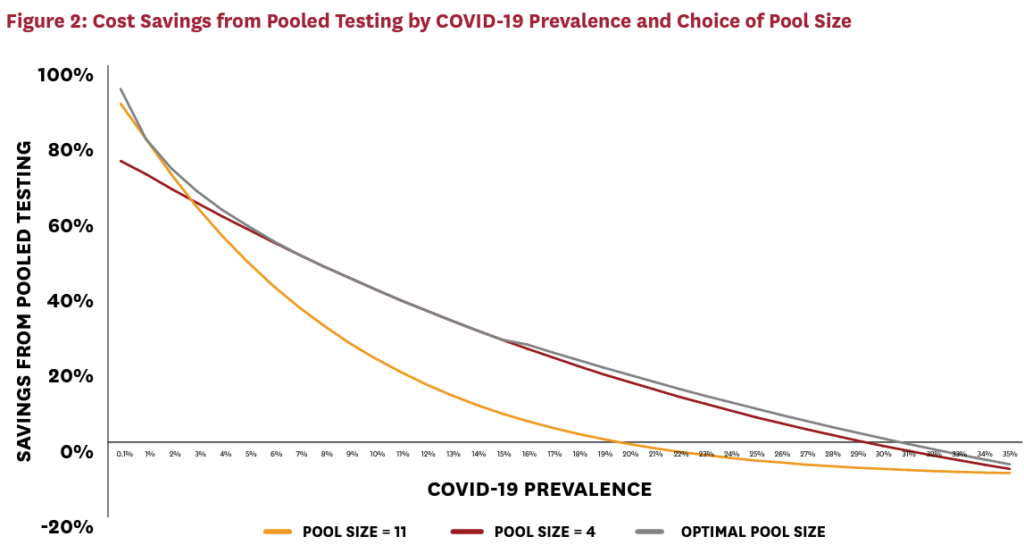
Figure 2 explores this issue in more detail. The figure plots cost savings per worker, relative to individual testing, as a function of COVID-19 prevalence and the pool-size strategy selected. For example, if an employer knows that COVID-19 prevalence is 1 percent, the optimal pool size of 11 can save 80 percent over the strategy of testing all workers individually. The savings fall with prevalence, because pooled testing works best with large numbers of disease-free pools. Nonetheless, even at extremely high COVID-19 infection rates, employers can save 30 percent via pooled-testing strategies.
Figure 2 presents three curves that correspond to different pool-size selection strategies. The gray optimal pool size curve presents what happens when employers know the underlying COVID-19 prevalence and can perfectly solve the cost-minimization problem given earlier. This is the maximum cost saving that can be achieved for any given level of COVID-19 prevalence. In contrast, the cardinal and orange curves illustrate how much employers can save simply by setting pool sizes of four and 11, respectively. Interestingly, the pool size of four captures the vast majority of savings unlocked by optimal decision-making even when prevalence is very small. This suggests that employers can still harvest substantial gains from pooled testing, even when they do not have good information about underlying COVID-19 prevalence. For example, four-person pools save roughly 75 percent of costs for an employer with virtually no prevalence. Pool sizes larger than four — even for this employer with negligible illness prevalence — can save at most 25 percent more in incremental costs.
The orange curve presents a cautionary tale, however. If employers respond to uncertainty by erring on the side of large pools, this could be costly in the event that their actual prevalence is high. The worst-case scenario for the four-worker pool strategy is to take cost savings down from 80 percent to 71 percent. In contrast, the worst-case scenario for the 11-worker pool could involve cost increases over universal individual testing — indeed, at 20 percent prevalence, the 11-worker pool results in very slightly negative savings over universal individual testing. Note also that pooling saves money for all active infection rates less than 30 percent, which is a remarkably broad range, likely to contain nearly all real-world cases.
The lesson here is that employers can reap meaningful gains from four-worker pools at levels of prevalence below 20 percent. Employers with particularly good prior information about COVID-19 prevalence may be able to reap even larger gains by expanding their pool sizes, but they could stand to lose out on substantial gains if they are wrong about their underlying infection rates.
Reliability of Pooled Testing
So far, COVID-19 testing remains imperfect. We now consider the implications of imperfect test reliability for the size of pools and the extent of possible cost savings. Define σN as the probability that a true negative sample returns a negative test. This is the “specificity” of the test, and 1-σN is the associated false-positive rate. Analogously, define σP as the probability that a true positive sample tests positive. This is the “sensitivity” of the test, and 1-σP is the associated false-negative rate. We assume here that the sensitivity and specificity of the test are the same when applied to a pooled sample as to an individual sample. While pooled samples might degrade the reliability of tests — e.g., by reducing the concentration of the virus in a sample — existing evidence suggests that our simplification does not sacrifice much generality. Specifically, existing research on pooled COVID-19 testing suggests that for pool sizes below 16 the test degradation is relatively limited.13
Nonetheless, even if pooling does not degrade test reliability, the sensitivity and specificity of a pooled-testing protocol will be different than those of a single-patient testing protocol. In this section, we explain why this is so, and we characterize the associated reliability of a pooled-testing approach. We also discuss how to improve pooled-testing reliability, and perform some numerical analyses to judge the cost and pool-size implications.
mplications. The source of testing errors matters for the reliability of pooled testing. Errors that occur during specimen collection are less problematic for pooled testing than errors that occur during test processing. If an individual provides a “bad” specimen, pooled testing mitigates some of the consequences, because that individual might be pooled with an infected individual that provided a “good” specimen. As such, the result of the pooled test is not compromised, even though individual test results would have been. In contrast, consider the case where a lab makes an error in processing a pooled specimen. This error invalidates the test for an entire pool of people, making it more harmful than a similar error perpetrated on a single person’s test. We begin our analysis by assuming that all errors are of the “worst-case scenario” form that affects the entire pooled sample. We then explore the improvements in reliability that would occur if errors instead occur at the specimen collection level.
Specificity of Pooled Testing
Consider the case of a true-negative patient. The probability that they will test negative yields the test’s specificity. Under individualized testing, the probability of an accurate test is σN and so is the test specificity. To construct the associated specificity under pooling, notice that the true-negative patient receives a negative test result if: 1) their pooled sample tests negative; or 2) their pooled sample tests positive, but their individual follow-up test comes up negative. As before, define the pool size as P and the prevalence as π. Since this patient is already truly negative by assumption, the probability of their pool being truly negative is given by (1-π)(P-1), and the probability of the pool being positive is 1-(1-π)(P-1). As discussed above, we start by assuming that testing errors consist of the entire pooled sample being mishandled. That is, we assume that an error impacts every member of the sample – i.e., testing errors are perfectly correlated within the sample. Therefore, the probability of a negative pooled test result is:
(1-π)(P-1) σN +(1-(1-π)(P-1))(1-σP ).
This is the probability of a true-negative result plus the probability of a false-negative test result. Similarly, the probability of a positive pooled-test result can be constructed as:
[(1-(1-π)(P-1) ) σP +(1-π)(P-1) (1-σN )].
This is the probability of a true-positive result plus the probability of a false-positive result.
In light of these expressions, the probability that our true-negative patient tests negative in a pooled-testing strategy is:
(1-π)(P-1)σN + (1-(1-π)(P-1))(1-σP ) + [(1-(1-π)(P-1))σP + (1-π)(P-1)(1-σN )]σN = [σN σP + (1-σP )] + (1-π)(P-1)[σN – σN^2 – 1 + σp + (1 – σP )σN ].
Some algebraic manipulation proves that this “pooled specificity” exceeds the underlying test specificity, σN .viii As a result, pooled testing increases testing specificity and reduces the probability of false positives. Intuitively, the pooled test creates an additional hurdle for a false-positive result, because the true-negative patient must end up both with a positive pooled test and an inaccurately positive individual test. The additional hurdle of the pooled test reduces the chances of false positives.
Sensitivity of Pooled Testing
These benefits of pooling for test specificity come at the cost of reduced sensitivity. Consider the alternative case of a true-positive patient. Under individualized testing, the probability of an accurate positive test is σP , which is also the test sensitivity. Under pooled testing, this patient receives an accurate result if their pool tests positive and their follow-up test comes up positive. Since this individual is a true positive, their pool is also truly positive. Therefore, the probability of a positive pooled test is σP . This individual will test positive if their pool tests positive, and they then test positive in the individual testing round. Therefore, the probability that this true-positive individual ends up testing positive is σP^2 . To reiterate, we are still assuming the worst-case scenario of correlated testing errors within the pool.
Notice that pooling reduces the sensitivity of testing by the factor σp . For example, if the sensitivity of the underlying test is 90 percent, the sensitivity of a pooled approach will be 81 percent, and so on. This degradation can become quite problematic in real-world applications. For example, suppose the sensitivity of the underlying test is 70 percent; as we noted earlier, this is a realistic estimate for COVID-19 testing at present. In this case, pooling approaches would yield a true sensitivity of 49 percent, which is worse than a coin flip.
Absent improvements in the underlying assay technology, one feasible solution is to perform multiple tests on the pooled samples. In particular, suppose we were to run two independent tests on a pair of pooled samples from the same pool. In this case, the true-positive patient will receive an individual test if either pooled test turns up positive. Therefore, the probability that the true-positive patient tests positive will be:
σP^2 + (1-σP )σP^2 = σP^2 (2-σP ) >σP^2
In this case, for an assay with an underlying sensitivity of 70 percent, the sensitivity of the pooled-testing protocol will be 63.7 percent, significantly better than the 49 percent sensitivity produced by pooled testing without a confirmatory round.
Clearly, however, multiple rounds of pooled testing will reduce the cost savings achievable via pooling. Moreover, since it is now costlier to test more pools, it will also increase the optimal pool size. We now quantify these effects via numerical analysis of the problem.
Economics of Imperfected Pooled Testing with Sample Processing Errors
As above, suppose we conduct a second round of testing on every pooled sample. Therefore, define the true-positive rate for a pool as TP ≡ σP (2 – σP ); this is the probability that a true-positive pool tests positive after two independent rounds of testing. Analogously, define the false-positive rate for a pool as FP ≡ (1+σN ) (1-σN ), which is the probability that a true-negative pool tests positive after two rounds of testing.
Conservatively, we assume that two rounds of testing on each pool doubles the cost of the pooled-testing stage. Therefore, testing cost per worker with two tests per pool is given by:
(2τC )/P+{(1-(1-π)P ) T_P+(1-π)P F_P } τ_C.
This can be simplified as:ix
(2τC )/P+{T_P+(1-π)P (F_P-T_P)} τ_C.
This is the objective function we will minimize. Analytically, it remains true that higher prevalence, π, leads to higher optimal pool sizes. It can also be shown that, compared to the single round of pooled testing, adding a confirmatory round increases the optimal pool size. Intuitively, confirmatory testing increases the relative cost of the pooled round compared to the individual round. Therefore, there is an incentive to economize on the number of pools by expanding their sizes.
Numerical Analysis of Imperfect Testing with Sample Processing Errors
We now calculate the optimal group size and cost savings associated with imperfect testing. For concreteness, we assume that σP = 70%, so that the false negative rate is 30 percent. And, we assume that σN = 99%, so that the false positive rate is 1 percent.
Figure 3 demonstrates that imperfect testing with these parameters roughly doubles the optimal group size, compared to the perfect testing case. The cost of testing each pooled sample has doubled, so the optimal response is to reduce the number of pools. While this response mitigates some of the cost impact, imperfect testing somewhat limits the cost savings achievable via pooling. Figure 4 illustrates the implications for cost savings.
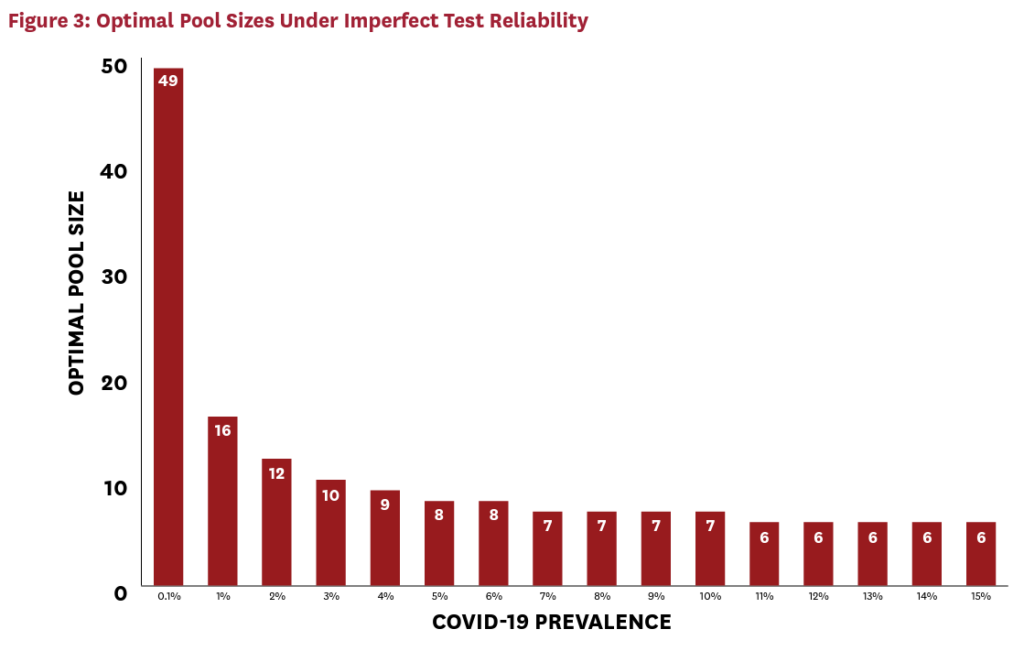
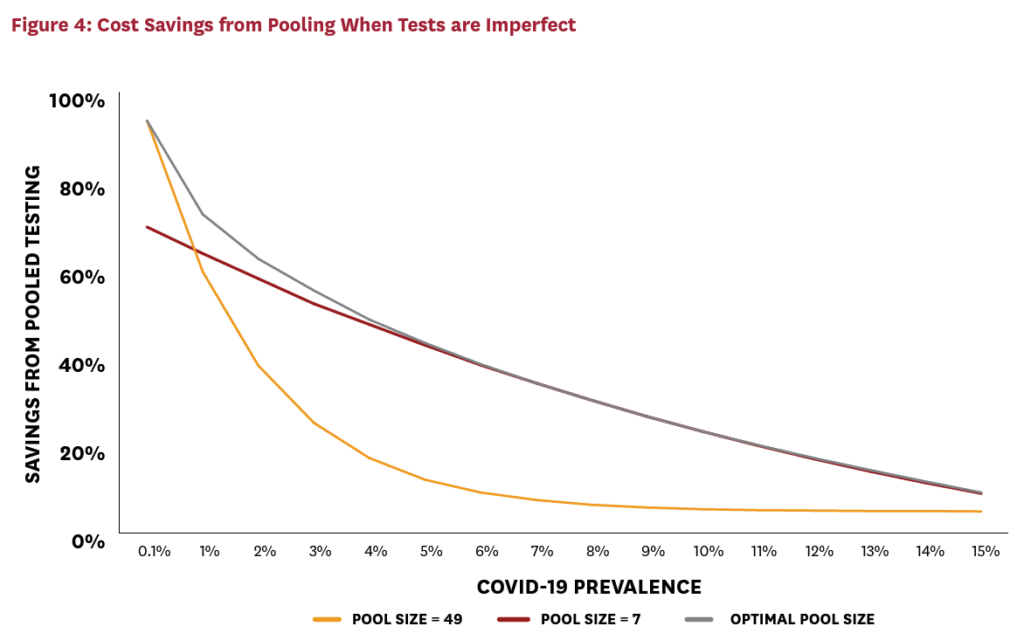
For a given active infection rate, cost savings have fallen. For example, at a prevalence of 4 percent, roughly 60 percent can be saved with a perfect test. With imperfect test reliability, this falls to just below 50 percent. (Less reliable tests requiring additional confirmatory rounds would naturally drive this number down even further.) While this is a nontrivial increase in costs, it is far less than proportional to the doubling of the pooled-test cost. This is because the costs of the pooled tests represent only a fraction of total testing costs, and because the growth in pool sizes partially mitigates the effect on costs. Moreover, even with imperfect tests, pooled testing remains viable for many localities in the United States. Significant savings can be achieved for localities with active infection rates below 10 percent, and some savings are achievable with active infection rates as high as 15 percent. Moreover, in the case of imperfect testing, a pool size of seven performs reasonably well at capturing the lion’s share of cost savings, even when prevalence is uncertain. This illustrates that higher “rule-of-thumb” pool sizes are necessary when tests are imperfect to mitigate the cost-increasing effects of imperfect testing.
Specimen Collection Errors
The analysis above considered a “worst-case scenario” for the impacts of testing errors. We assumed that errors occur at the level of the pool, not the individual contributing to the pool. In other words, the testing error affects everyone in the pool at the same time — it is “perfectly correlated.” For the sake of concreteness, a lab that mishandles an entire sample creates a perfectly correlated error. A piece of testing equipment that occasionally delivers an inaccurate result does the same. However, as discussed above, some or even many testing errors in a pooled context might be uncorrelated across the pool members. An example is an improper specimen collection – e.g. from a poorly executed nasal swab. Unless all members of the pool are swabbed by the same person using the same poor technique, swabbing error may not propagate to the entire pool. This is the case of “uncorrelated” testing error, or what we refer to as “specimen” error. To illustrate the effects of correlatedness in testing error, we consider perfectly uncorrelated specimen errors as a counterpoint to the earlier discussion of perfectly correlated sample processing errors.
Under individual testing, test specificity – i.e., the probability of a positive patient receiving a positive test result — was σP . Under a single-round of pooled testing with sample processing errors, this probability fell to σP^2 . We showed that investing in a confirmatory testing round would increase this probability to σP^2 (2 – σP ). We now study what happens to specificity when errors are due entirely to specimen collection.
Mathematically, consider the case of a true-positive person participating in a pool. The probability that each other individual pool member contributes a negative sample is given by [(1-π) σN +π(1-σP )]. This is the probability of being a true negative, plus the probability of being a false negative. Therefore, the full probability of the pool testing positive — conditional on the presence of at least one true-positive member — is given by:
σP + (1 – σP ){1 – (1 – π)σN + π(1 – σP ) } > σP .
The left-hand side reflects the probability of two separate states: 1) the true positive person contributes an accurate sample, which has probability (1 – σP ); and 2) the true positive person contributes an inaccurate sample, but someone else in the pool tests positive.
With correlated errors, the sensitivity of the initial pooled test was simply σP , which is independent of the pool size. When errors are uncorrelated, however, the sensitivity improves with the size of the pool because more pool members are providing “insurance” against a false result for the pool as a whole. Indeed, the expression above indicates that, as pool size approaches infinity, sensitivity approaches 100 percent. While this is not a realistic case, it does demonstrate that pool-size growth always improves the sensitivity of the pooled-testing round.
Of course, the outcome of interest is whether this true positive person ultimately tests positive himself. The probability of this happening is exactly σP , which is identical to what it would be under individual testing. To see why, recall that we can segment all outcomes into two mutually exclusive sets: 1) the true positive person contributes an accurate sample, or 2) the true positive person contributes an inaccurate sample. In the first case, the true positive person always receives a positive test result, because the pooled sample will test positive, and so will the individual follow-up. However, in the second case, the true positive person never receives a positive test result, because her follow-up test will always come back negative. Therefore, since the probability of the first case is σP, it follows that the total sensitivity of pooled testing in this case is σP .
In reality, testing errors arise from specimen collection and sample processing. Without more detailed information about the relative importance of each error type, it is difficult to pin down the exact reliability measures. However, our analysis provides some bounds for the reliability of pooled testing. In the best-case scenario, with specimen collection errors only, pooled testing is just as reliable as individual testing. In the worst-case scenario, with sample-processing errors only, pooled testing exhibits much lower sensitivity, but this issue can be mitigated via confirmatory testing of the pooled sample.
Implications
The economic shutdown from COVID-19 continues to impose enormous costs, even as it produces very large survival and health benefits.18 Counting up the economic damage at this early stage poses considerable challenges, but preliminary estimates suggest that each month of shutdown hacks 5 percent (or about $1 trillion) off our annual GDP.19 In contrast, testing every American worker, even at a per-worker cost of $500, results in the comparatively “small” cost of around $60 billion. Nonetheless, if this cost ends up falling on American businesses and school systems, already crippled in the aftermath of a major shutdown, even more economic damage could result. Finding cost-effective ways to test might provide a way out of the shutdown.
Our estimates suggest that pooled testing could lower testing costs by half or even three-quarters for many schools and businesses, with an acceptable loss in test sensitivity. The result could be tens of billions of dollars saved, and even more if firms need to test workers repeatedly over the course of the epidemic. This strategy could be particularly beneficial for employers who feel compelled to test employees frequently — such as those in close contact with the public — especially if prevalence among these workers is low.
As new and better information about prevalence arrives, savings will likely increase. However, the deep uncertainty around infection prevalence today should not deter businesses from employing pooled tests. Simple strategies of pooling four to seven workers could save businesses 50–60 percent over standard individualized testing.
From a macroeconomic perspective, pooled testing could bump GDP growth numbers up by 20 percent or more. For instance, at Medicare rates, PCR testing costs $50 to $100.20,5 With roughly 160 million Americans in the labor force, at the upper end, each wave of COVID19 testing costs around $16 billion. If pooled testing helps employers realize 50 percent savings on these costs, this generates $8 billion per wave of testing that accrues to the bottom lines of American businesses. If testing is repeated bimonthly — roughly the length of one quarantine period — the annual savings of $192bn amounts to 0.8 percent of total GDP. In 2019, GDP grew by 2.3 percent.21 Thus, pooled testing could save about two-fifths of the economic growth we experienced in 2019. Since 2020 is likely to be a much leaner year, the effects will be even more dramatic.
As noted above, concerns persist about diagnostic accuracy, particularly the high probability of false negatives, coupled with the risk of high costs that such false negatives can create. Employers can consider implementing testing in conjunction with other monitoring strategies, such as symptom monitoring and contact tracing. Moreover, testing technology is advancing rapidly, which will likely increase sensitivity and reduce costs, complexity and discomfort. For example, recent evidence suggests that saliva-based tests may be a suitable alternative to nasal swabs, and companies are working to develop high-capacity, rapid testing technologies.15,22
Pooling is a well-established method to perform tests cost effectively and at a much greater scale than is currently feasible, with an acceptable loss of sensitivity. Many experts have pointed to frequent and widespread testing as a prerequisite for a return to economic normalcy.23 Pooled testing — even in groups as small as four — will allow employers and schools to conserve scarce resources, save money and get Americans back to business.
Footnotes
i In contrast, serology tests are designed to determine the presence of antibodies, or whether someone has been infected in the past. Complementary serology testing could potentially be used to excuse immune individuals from the need for active-virus testing, though research is still ongoing to determine whether antibodies fully protect people from reinfection. ii In this paper, we focus on the lab fees of the test itself, rather than the cost of sample collection, which is not necessarily affected by pooled samples, depending on how sample collection is deployed.
iii Note that we abstract from false negatives or false positives in the testing process. These can be incorporated into the model by allowing for confirmatory testing in subsequent steps.
iv Assuming continuous pool sizes, the first-order condition for optimal pools is -(1/P^2 ) – ln(1-π)(1-π)P = 0. Comparative statics then imply that -(2/P^3 ) – (ln(1-π) )2 + [(1+P(ln(1-π) ))/(1-π) ] = 0. Since ln(1-x)<-x, it follows that ([(1+P(ln(1-π) ))/(1-π) ]<((1-Pπ)/(1-π) ) ≤ 0, where strict equality holds for all nontrivial group sizes W_G>1. If the second-order condition holds, then the term in square brackets is positive. Therefore, for any local minimum with nontrivial pool size P>1, it follows that (dP/dπ ) < 0. In 0. Since pool sizes are integer-valued, there will be regions where increases in prevalence leave the optimal integer-valued P unchanged. The numerical analyses explore this issue in more detail.
v Notice that (dT/dπ ) = NτC(1-π)(P-1) > 0.
vi Define π* (P) as the maximum prevalence at which a pool size of P weakly reduces costs. Therefore, 1/P + (1-(1-π* (P))P) = 1. This implies that π(P) = 1-(1/P )^(1/P ). It is straightforward to verify numerically that P=3 results in the highest possible value of π across integer values of P, and that π*(P)=1-(1/3 )^(1/3 ) ≈ 30.66.
vii The mathematics here are not new, as similar calculations are presented in Dorfman (1943).
viii To see why, first notice that [σN σP +(1-σP )] is a weighted average of σN and unity. The term [σN – σN^2 – 1 + σp + (1 – σP )σN ] can be either negative or positive. If it is positive, the result follows immediately. If, however, it is negative, then: [σN σP + (1 – σP )] + (1-π)(P-1)[σN – σN^2 – 1 + σp + (1 – σP )σN ] > [σN σP + (1 – σP )] + [σN – σN^2 – 1 + σp + (1 – σP )σN ] = σN (2 – σN ) > σN
References
- Dorfman, R. (1943). The detection of defective members of large populations. The Annals of Mathematical Statistics, 14(4), 436-440.
- Baker, P., Barker, K., Blinder, A., et al. (2020, April). Trump’s remarks prompt warnings on disinfectants. New York Times. https://www.nytimes.com/2020/04/24/us/coronavirus-us-usa-updates.html.
- Kotlikoff, L. (2020, March 29). Group testing is our surefire secret weapon against coronavirus. Forbes. https://www. forbes.com/sites/kotlikoff/2020/03/29/group-testing-is-our-secret-weapon-against-coronavirus/#13c75b8c36a6.
- U.S. Department of Labor Occupational Safety and Health Administration. (2020). Guidance on preparing workplaces for COVID-19. https://www.osha.gov/Publications/OSHA3990.pdf.
- Centers for Medicare & Medicaid Services. (2020). Press release: CMS increases Medicare payment for high-production coronavirus lab tests. https://www.cms.gov/newsroom/press-releases/cms-increases-medicare-payment-highproduction-coronavirus-lab-tests-0.
- The White House, Centers for Disease Control and Prevention, Food and Drug Administration. (2020). Testing Blueprint: Opening Up America Again. https://www.whitehouse.gov/wp-content/uploads/2020/04/Testing-Blueprint. pdf.
- Bender, M. C., & Abbott, B. (2020, April). Trump Administration has enough tests for 2% of each state’s population, official says. Wall Street Journal. https://www.wsj.com/articles/trump-administration-has-enough-tests-for-2-ofpopulation-official-says-11588009570.
- Allen, D., Block, S., Cohen, J., et al. (2020, April). Roadmap to pandemic resilience: Massive scale testing, tracing, and supported isolation (TTSI) as the path to pandemic resilience for a free society. Edmond J. Safra Center for Ethics at Harvard University. https://ethics.harvard.edu/files/center-for-ethics/files/roadmaptopandemicresilience_ updated_4.20.20_0.pdf
- Conger, K. (2020, April). Testing pooled samples for COVID-19 helps Stanford researchers track early viral spread in Bay Area. Stanford Medicine News Center. http://med.stanford.edu/news/all-news/2020/04/testing-pooled-samples-totrack-early-spread-of-virus.html.
- HospiMedica International Staff Writers. (2020, March). Israeli researchers introduce pooling method for COVID-19 testing of over 60 patients simultaneously. HospiMedica International. https://www.hospimedica.com/coronavirus/ articles/294781273/israeli-researchers-introduce-pooling-method-for-covid-19-testing-of-over-60-patientssimultaneously.html.
- Schmid-Burgk, J. L., Li, D., Feldman, D., et al. (2020, April). LAMP-Seq: Population-scale COVID-19 diagnostics using a compressed barcode space. BioRxiv, 2020.04.06.025635. https://doi.org/10.1101/2020.04.06.025635.
- Keeler E. & Berwick D. (1976). Effects of pooled samples. Health Laboratory Science, 13(2), 121–28. https://www.ncbi. nlm.nih.gov/pubmed/1270261.
- Yelin, I., Noga Aharony, N., Shaer-Tamar, E., et al. (2020, March). Evaluation of COVID-19 RT-qPCR test in multisample pools. MedRxiv. https://doi.org/10.1101/2020.03.26.20039438.
- Yang Y., Yang, M., Shen, C., et al. (2020, February). Evaluating the accuracy of different respiratory specimens in the laboratory diagnosis and monitoring the viral shedding of 2019-nCoV infections. MedRxiv. https://doi.org/10.1101/20 20.02.11.20021493.
- Wang, W., Xu, Y., Gao, R., et al. (2020, March). Research letter: Detection of SARS-CoV-2 in different types of clinical specimens. JAMA. doi:10.1001/jama.2020.3786.
- Pratt, E. (2020, April 13) ‘False negatives’ in COVID-19 testing: If you have symptoms, assume you have the disease. Healthline. https://www.healthline.com/health-news/false-negatives-covid19-tests-symptoms-assume-you-have-illness.
- Aprahamian, H., Bish, E. K., & Bish, D. R. (2017). Adaptive risk-based pooling in public health screening. IISE Transactions, 50(9), 753–66. https://doi.org/10.1080/24725854.2018.1434333.
- Joyce, G. (2020, April 25). Are we overreacting to the coronavirus? Let’s do the math. MarketWatch. https://www. marketwatch.com/story/are-we-overreacting-to-the-coronavirus-lets-do-the-math-2020-04-19.
- Makridis, C., & Hartley, J. (2020). The cost of COVID-19: A rough estimate of the 2020 US GDP impact. Mercatus Center, George Mason University. COVID-19 Policy Brief Series. https://www.mercatus.org/publications/covid-19policy-brief-series/cost-covid-19-rough-estimate-2020-us-gdp-impact.
- Irfan, U. (2020, April 2). How Covid-19 immunity testing can help people get back to work. Vox. April 2. https://www. vox.com/2020/3/30/21186822/immunity-to-covid-19-test-coronavirus-rt-pcr-antibody.
- Bureau of Economic Analysis. (2020, March 26). News release: Gross domestic product, fourth quarter and year 2019 (third estimate); corporate profits, fourth quarter and year 2019. https://www.bea.gov/news/2020/gross-domesticproduct-fourth-quarter-and-year-2019-third-estimate-corporate-profits.
- Laraki, O. (2020, March 31). Mobilizing Color’s infrastructure in response to the COVID-19 crisis. Color blog. https:// www.color.com/mobilizing-colors-infrastructure-in-response-to-the-covid-19-crisis.
- Romer, P., & Garber, A. M. (2020, March 23). Opinion: Will our economy die from coronavirus? New York Times.

You must be logged in to post a comment.